쌓고 쌓다
[자료구조] 이진 탐색 트리 삭제연산 (반복문) 본문
전체 코드
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode
{
int key;
TreeNode* left, * right;
}TreeNode;
void delete_node(TreeNode** root, int key)
{
TreeNode* p, * child, * succ, * succ_p, * t;
// key를 갖는 노드 t(arget)를 탐색, p는 t의 부모
p = NULL;
t = *root;
while (t != NULL && t->key != key)
{
p = t;
t = (key < t->key) ? t->left : t->right;
}
if (t == NULL)
{
printf("트리에 키가 존재하지 않음.");
return;
}
if (t->left == NULL && t->right == NULL)
{
if (p->left == t)
p->left = NULL;
else
p->right = NULL;
}
else if (t->left == NULL || t->right == NULL)
{
child = t->left != NULL ? t->left : t->right;
if (p != NULL)
{
if (p->left == t)
p->left = child;
else
p->right = child;
}
else // p가 NULL인 경우는 삭제 노드가 루트인경우
*root = child;
}
else
{
succ_p = t;
succ = t->right;
while (succ->left != NULL)
{
succ_p = succ;
succ = succ->left;
}
if (succ_p->left == succ) // (1) , s의 오른쪽만 있을것이다.
succ_p->left = succ->right;
else // (2)
succ_p->right = succ->right;
t->key = succ->key;
t = succ;
}
free(t);
}
int main(void)
{
}
함수 delete_node
void delete_node(TreeNode** root, int key)root에는 원래 트리의 루트의 포인터가 넘겨집니다.
key는 찾을 값을 입력
TreeNode* p, *child, *succ, *succ_p, *t;
// key를 갖는 노드 t(arget)를 탐색, p는 t의 부모
p = NULL;
t = *root;t : key를 갖는 노드를 탐색
p : t의 부모
처음에 루트를 t에 넣습니다.
루트의 부모는 없으므로 p는 NULL입니다.
while (t != NULL && t->key != key)
{
p = t;
t = (key < t->key) ? t->left : t->right;
}이 while문은 t가 NULL이거나 t가 키를 찾았을 때 탈출합니다.
이때 탈출할시 p는 t의 부모를 가리킵니다.
p를 t로 바꾸고 t 또한 내려갈 것인데
목표로 하는 key가 현재 탐색 중인 노드 t의 Key보다 작을 경우 t의 left로 t를 옮깁니다.
결과적으로 t가 NULL이거나 t가 타겟을 찾아 가리키고 있겠지요.
if (t == NULL)
{
printf("트리에 키가 존재하지 않음.");
return;
}t가 NULL인 경우 타겟을 못 찾은 거니 해당 트리에 원하는 key가 없는 것입니다.
이제 아래부터의 코드는 삭제할 노드를 찾은 경우로 t에는 삭제할 노드가 담겨있습니다.
삭제할 때 3가지의 경우가 존재합니다.
- 삭제하려는 노드가 단말 노드인 경우
- 삭제하려는 노드가 왼쪽 또는 오른쪽에 서브 트리가 하나만 존재하는 경우
- 삭제하려는 노드가 양쪽으로 서브 트리를 가지고 있을 경우
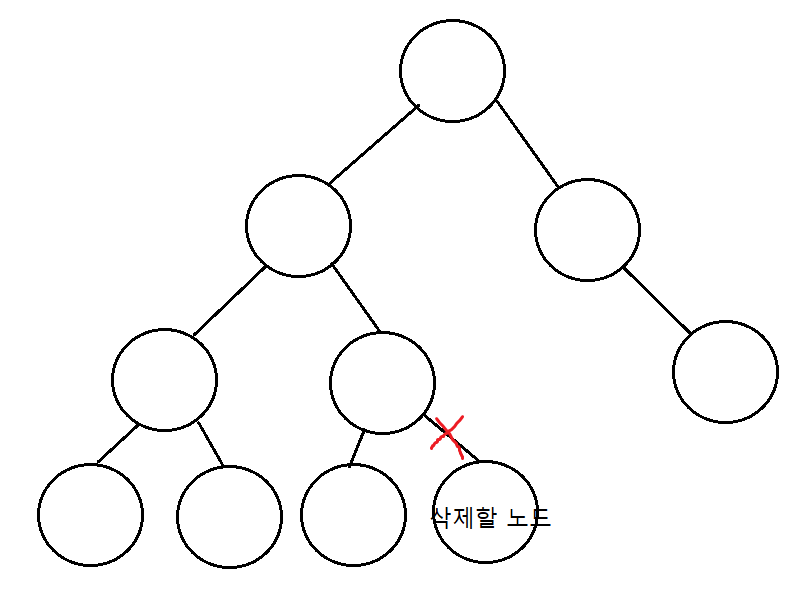
CASE 1)
그냥 간단히 단말 노드의 부모를 찾아 연결을 끊어주면 됩니다.
if (t->left == NULL && t->right == NULL)
{
if (p->left == t)
p->left = NULL;
else
p->right = NULL;
}단말 노드인 경우 t의 left right는 NULL일 테니 이 if문에 걸리게 됩니다.
p는 t의 부모로 p의 left가 t인 경우 p의 left를 NULL로
p의 right가 t인 경우 p의 right를 NULL로 초기화합니다.
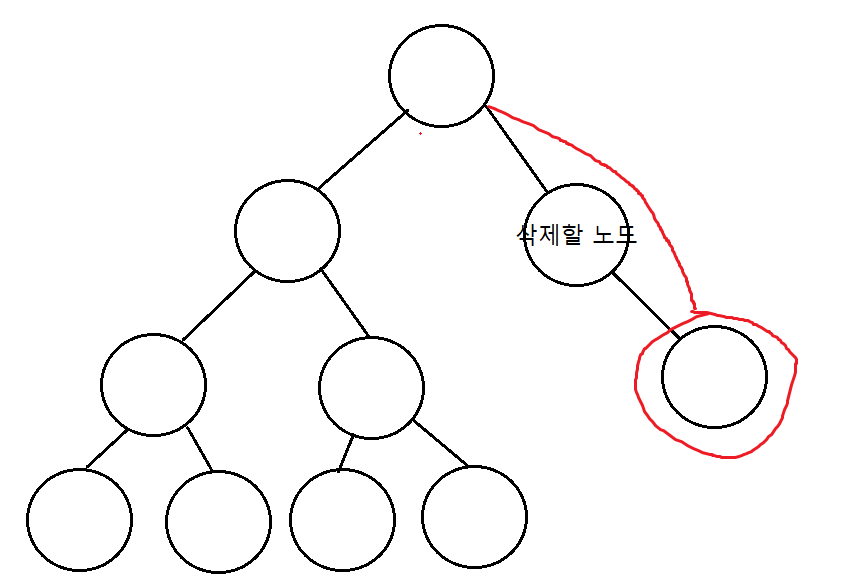
CASE 2)
삭제하려는 노드가 하나의 서브 트리만 갖는 경우입니다.
그냥 삭제하려는 노드를 삭제하고 서브 트리는 부모 노드(p)에 붙여주면 됩니다.
else if (t->left == NULL || t->right == NULL)
{
child = t->left != NULL ? t->left : t->right;
if (p != NULL)
{
if (p->left == t)
p->left = child;
else
p->right = child;
}
else // p가 NULL인 경우는 삭제 노드가 루트인경우
*root = child;
}left 또는 right중 하나가 NULL인 경우 이 if문에 걸립니다.
child는 t의 child를 가리킬 것이고
t의 left가 NULL이 아닌 경우 left에 하나의 서브 트리가 존재하는 것이므로 child를 t->left로
반대로 t의 left가 NULL인 경우 right에 서브 트리가 있을 거니 이것을 child로 넣어줍니다.
p가 NULL이 아니라면 삭제할 노드가 부모가 있는 것으로 삭제할 노드는 루트가 아닌 게 되고
p의 left가 t인 경우 삭제당할 t가 p의 left에 있는 것이므로
그 자리를(p의 left)를 child로 채웁니다.
반대로 p의 right가 빵꾸가 난 경우
그 자리를(p의right)를 child로 채웁니다.
만약, p가 NULL인 경우 삭제할 노드가 루트이므로
루트를 그냥 child로 가리키게 합니다.
CASE 3)
삭제하려는 노드가 두 개의 서브 트리를 갖고 있는 경우로
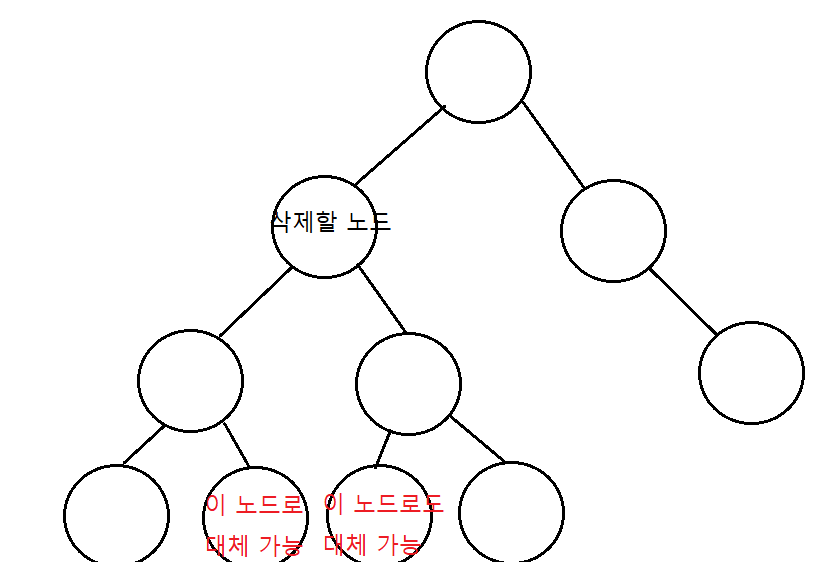
삭제할 노드를 대체할 후보자가 두 개가 가능합니다.
이 두 후보자 노드 중 뭘 와도 가능한데 오른쪽 서브 트리의 가장 작은 노드를 후보자로 지정하는 코드를 작성할 것입니다.
else
{
succ_p = t;
succ = t->right;
while (succ->left != NULL)
{
succ_p = succ;
succ = succ->left;
}
if (succ_p->left == succ) // (1) , s의 오른쪽만 있을것이다.
succ_p->left = succ->right;
else // (2)
succ_p->right = succ->right;
t->key = succ->key;
t = succ;
}succ_p는 후계자의 부모
succ는 후계자를 뜻합니다.
첫 후계자 부모는 t를 가리키고
후계자는 후계자 부모의 오른쪽 노드를 가리킵니다.
왜냐하면 후계자로 삭제할 노드의 오른쪽에서 가장 작은 노드를 찾을 것이기 때문입니다.
while문을 통해서 후계자의 left가 NULL일 때까지 쭉쭉 내려갑니다.
while문을 지나면 succ에는 삭제할 노드의 오른쪽 서브 트리 중 가장 작은 값이 들어있습니다.
succ_p에는 그 후계자의 부모를 가리킵니다.
만약 후계자 부모의 left에 후계자가 있다면 (1)의 그림으로
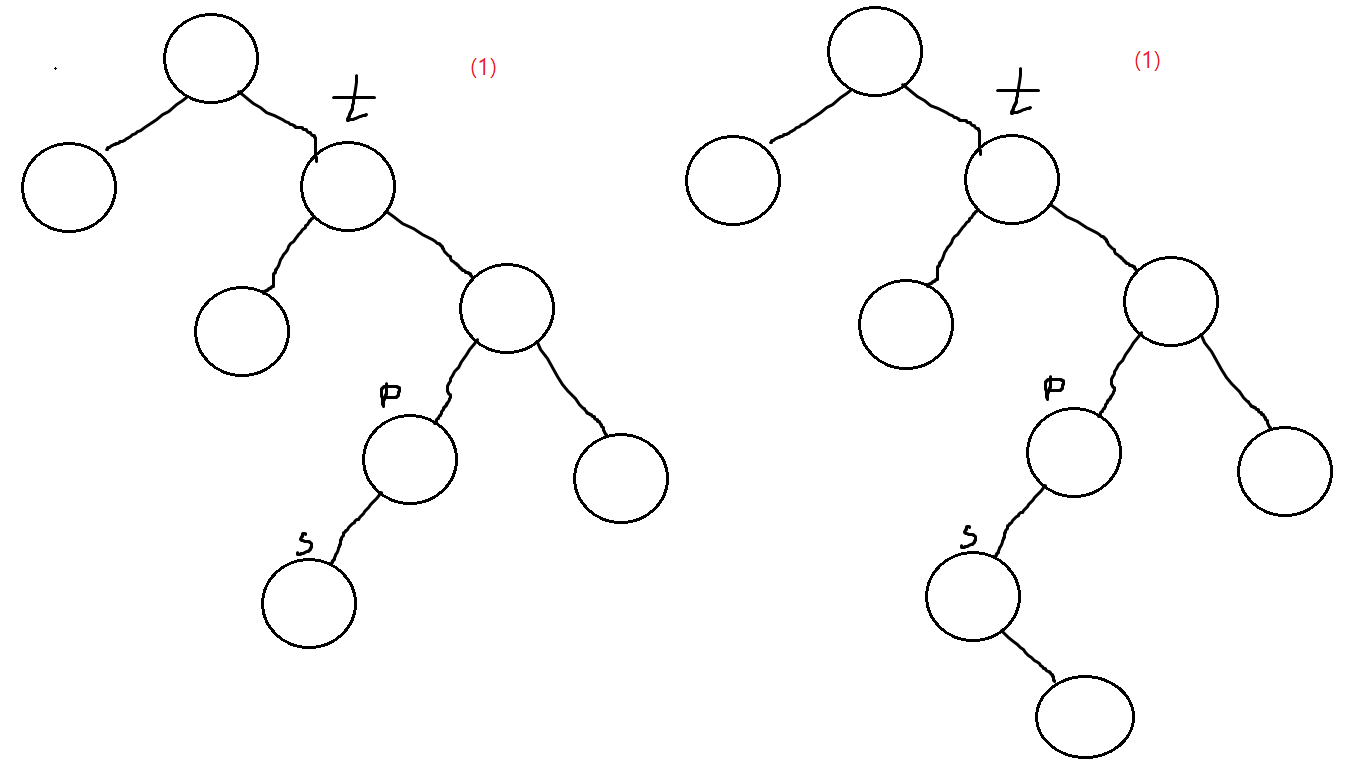
s의 right를 p의 left로 달아주면 되고 (추후에 삭제할 노드 t에 s의 값을 옮길 것임)
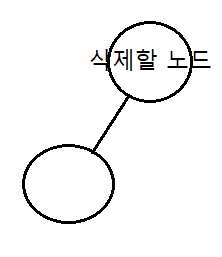
(2)는 t의 오른쪽 서브 트리가 바로 가장 작은 노드일 경우로 아래의 그림과 같습니다.
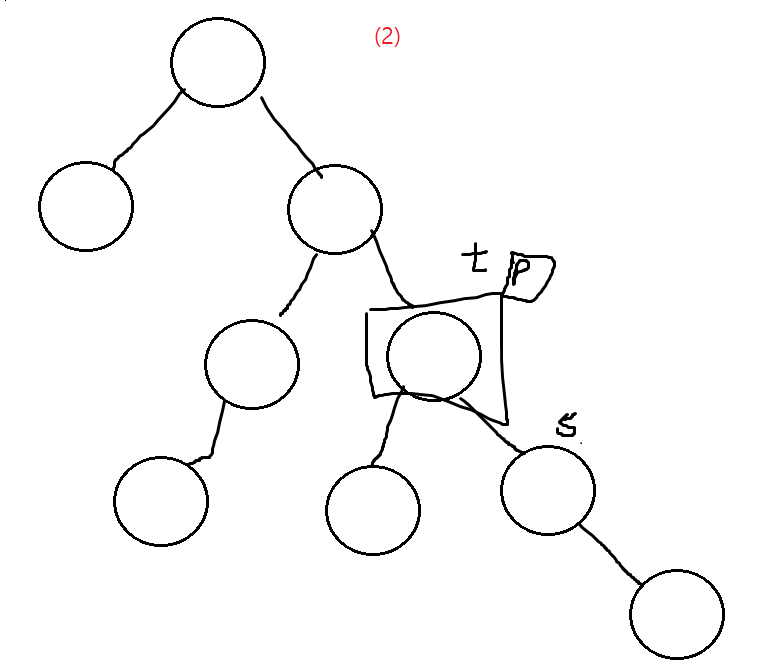
즉, 후계자 부모의 오른쪽에 후계자의 오른쪽 노드들을 붙여주면 됩니다.
t->key = succ->key;
t = succ;후계자 부모의 자식을 새로 연결시켜 준 이후로
삭제할 노드 t에 후계자의 값을 복사시켜주고
삭제할 노드는 후계자로 바꿔주면 됩니다.
삭제할 노드에 후계자의 값을 복사하고 후계자를 삭제하는 것으로 삭제의 결과를 얻을 수 있습니다.
삭제할 노드 t를 후계자 succ로 바꿔주면 됩니다.
모든 분기 조건들을 걸친 이후로 t에는 삭제할 노드가 담기고
그 t를 free로 삭제시켜줍니다.
그럼 삭제 연산의 완성입니다.
'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] Hash (0) | 2022.05.24 |
|---|---|
| [자료구조] 이진 탐색 트리의 삽입,삭제 (재귀함수) (0) | 2022.05.16 |
| [자료구조] 이진 탐색 트리 (탐색, 삽입) (0) | 2022.05.09 |
| [자료구조] 이진 트리의 순회 (0) | 2022.05.04 |
| [자료구조] 이진 트리 (0) | 2022.05.04 |




