쌓고 쌓다
[자료구조] Hash 본문
해싱
- 대부분 탐색 방법은 키 값 비교로 탐색하고자 하는 항목에 접근하지만 해싱은 바로 접근한다.
- 즉, 키 값에 대한 산술적 연산으로 테이블의 주소를 계산하여 항목에 접근
- key를 넣었더니 value가 나오는 것
해시 테이블(hash table)
: 키 값의 연산으로 직접 접근이 가능한 구조로 키 값으로 value를 찾는 것이다.
해시 함수(hash function)
- 키를 input으로 넣었더니 value로 해시 주소(hash address)를 생성하는 함수이다.
- 이 해시 주소가 배열로 구현된 해시 테이블(hash talbe)의 인덱스이다.

헤시 테이블 ht
- M개의 버켓(bucket)으로 구성된 테이블
- ht[0], ht[1], ... , ht[M-1]의 원소를 가짐.
- 하나의 버켓에 s개의 슬롯(slot) 가능
충돌(collision)
- 서로 다른 두 개의 탐색키 k1과 k2에 대해 해시함수에 넣었더니 같은 경우, 즉 h(k1)=h(k2)인 경우
오버플로우(overflow)
- 충돌이 버켓에 할당된 슬롯 수보다 많이 발생했을 경우 발생하는 것
- 오버플로우는 해결 방법이 필요하다.

간단한 해싱 예
-> 해싱으로 학생 정보를 저장, 탐색해보자.
- 5자리 학번이 있는데 앞 2자리는 학과, 나머지 3자리는 학과의 학생 번호이다.
- 같은 학과 학생들이라고 가정한다면 뒤의 3자리만 가지고 탐색이 가능하다.
- ex) 학번이 00023이면 이 학생의 정보는 ht[23]에 저장되어 있을 것이다.
- 탐색 시간이 O(1)이다.

위의 예제는 매우 이상적인 상황이고
실제로 해시 테이블의 크기가 제한적이므로, 모든 key에 대해 저장 공간을 할당할 수 없다.
또한 아래와 같이 총돌과 오버 플로우가 발생한다.
- h(k) = k mod M라고 가정하자. 무조건적으로 충돌과 오버플로우가 발생한다.

두 번째 예
- 알파벳 문자열 키의 해시함수가 키의 첫 번째 문자의 순서라고 가정
- 즉, a=0, b=1, c=2, ... 이런 식으로 value가 나오는 해시함수
- h("array") = 0
- h("binary") = 1 -> 이런 식으로 array, binary, bubble, file, digit, zero, bucket를 저장하자
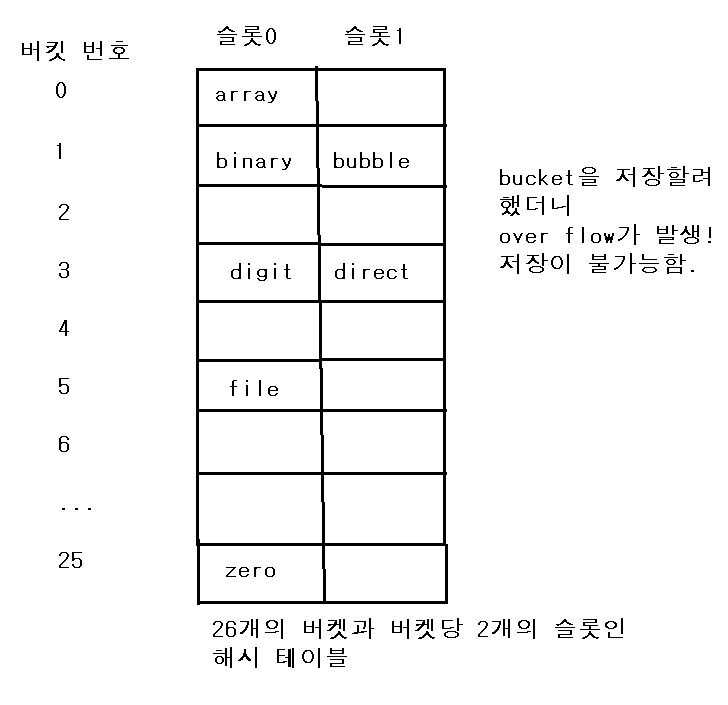
위의 예시들을 통해서 우리는 해시 함수가 잘 만들어져야 된다는 것을 알 수 있다.
아래의 조건이 좋은 해시 함수 조건이다.
- 충돌이 적음.
- 해시 함숫값이 해시 테이블의 주소 영역 내에 고르게 분포.
- 계산이 빠름.
해시함수 종류
제산 함수 (나머지 연산자)
- h(k) = k mod M
- 해시 테이블의 크기 M은 보통 소수(prime number)을 선택하는 것이 좋다.
폴딩 함수 (접지 함수)
- 이동 폴딩(shift folding) (이동 접지)
- 탐색 키를 여러 부분으로 나누어 값들을 더해 해시 주소를 얻는다.
- 경계 폴딩(boundary folding) (경계 접지)
- 탐색 키의 이웃한 부분을 거꾸로 더해 해시 주소를 얻는다.
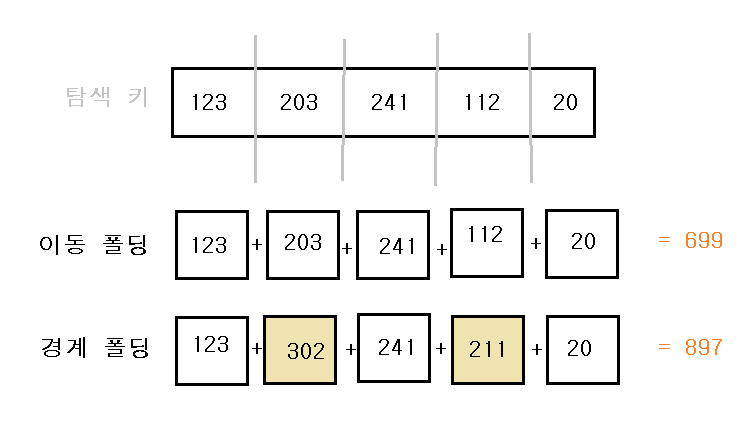
- 중간 제곱 함수
- 탐색 키를 제곱한 다음, 중간의 몇 비트를 뽑아 해시 주소 생성
- 비트 추출 함수
- 탐색키를 이진수로 간주하여 임의의 위치의 k개 비트를 해시 주소로 사용
- 숫자 분석 방법
- 키 중에서 편중되지 않는 수들을 해시 테이블의 크기에 적합하게 조합하여 사용
- 만약 학번이 있다면 2019에 입학한 숫자는 편중되어 있으니 해시 값 생성 시 제외한다.
충돌 해결 방법
- 충돌 : 서로 다른 탐색 키를 갖는 항목들이 같은 해시 주소를 가지는 현상
- 충돌이 발생하면 오버플로우가 발생한다.(슬롯이 꽉 차고 해시 테이블에 항목 저장 불가능)
- 오버플로우 해결 방법이 필요
오버 플로우 해결 방법
- 선형 조사법 (linear probing)
- 충돌이 일어난 항목을 해시 테이블의 다른 위치에 저장.
- 체이닝 (chaining)
- 각 버켓에 삽입과 삭제가 용이한 연결 리스트를 사용
선형 조사법
만약 충돌이 ht[k]에서 발생했다면 아래의 방법을 따른다.
- ht[k+1]이 비어있는지 조사한다.
- 또 안 비어있다면 ht[k+2]를 조사한다.
- 이것을 비어있는 공간이 나올 때까지 계속 반복
- 테이블의 끝에 도달했다면 다시 테이블의 처음부터 조사
- 조사를 시작했던 곳으로 다시 돌아왔다면 이것은 테이블이 가득 찬 것이다.
- -> 조사하는 위치 : h(k), (h(k)+1)%M, (h(k)+2)%M, ...
위의 방법으로는 군집화(clustering) 문제가 발생한다.
- 한번 충돌이 발생하면 그 위치에 항목들이 집중되는 현상 (왜냐 옆자리를 조사하기에)
- 탐색 시간을 증가시킨다.
(예1) h(k)=k mod 7
- 1단계 (8) : h(8) = 8 mod 7 = 1 (저장)
- 2단계 (1) : h(1) = 1 mod 7 = 1 (충돌 발생)
- ((h(1))+1) mod 7 = 2 (저장)
- 3단계 (9) : h(9) = 9 mod 7 = 2 (충돌 발생)
- (h(9)+1) mod 7 = 3 (저장)
- 4단계 (6) : h(6) = 6 mod 7 = 6 (저장)
- 5단계 (13) : h(13) = 13 mod 7 = 6 (충돌 발생)
- (h(13)+1) mod 7 = 0 (저장)
아래의 테이블처럼 저장됨
| 1단계 | 2단계 | 3단계 | 4단계 | 5단계 | |
| 배열 [0] | 13 | ||||
| 배열 [1] | 8 | 8 | 8 | 8 | 8 |
| 배열 [2] | 1 | 1 | 1 | 1 | |
| 배열 [3] | 9 | 9 | 9 | ||
| 배열 [4] | |||||
| 배열 [5] | |||||
| 배열 [6] | 6 | 6 |
충돌이 발생해 다른 곳에 저장된 데이터는 노란색으로 표시했다.
(예2) 문자열을 정수로 변환해 해시 주소 구하기
-> "do", "for", "if", "case", "else", "return", "function"을 저장해보자.
테이블의 크기는 13으로 M=13이다.
Ascii 코드값으로 해시 주소를 구할 것이다. ( a=97~z=122 )
해시 주소 = 합계 % 13
| 탐색 키 | 덧셈식으로 변환 | 합계 | 해시 주소 |
| do | 100+111 | 211 | 3 |
| for | 102+111+114 | 327 | 2 |
| if | 105+102 | 207 | 12 |
| case | 99+97+115+101 | 412 | 9 |
| else | 101+108+115+101 | 425 | 9 |
| return | 114+101+116+117+114 +110 |
672 | 9 |
| function | 102+117+110+99+116+105+111+110 | 870 | 12 |
아래의 테이블로 저장됨
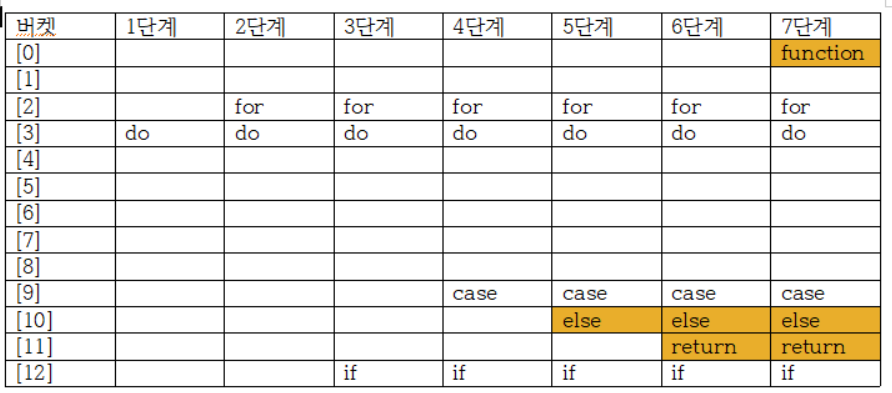
충돌이 일어나 제자리에 저장하지 못한 단어는 노란색으로 표시함.
이차 조사법(quadratic probing)
- 선형 조사법(linear probing)과 다르게 이차 함수에 의해 이동 폭을 넓혀가면서 사용함.
- 다음 조사할 위치를 ( h(k) + inc^2 ) mod M으로 구함 inc=0, 1, ... , M-1
- 조사되는 위치의 예 -> h(k), h(k)+1, h(k)+4, ...
- 선형 조사법에서의 문제점인 군집화(clustering) 완화
- 재해싱(rehashing)이라고도 함
- 오버플로우가 발생하면 원 해시함수와 다른 별개의 해시 함수를 사용.
- step = C-(k mod C) = 1+ k mod C -> 1부터 C 사이의 값을 생성
- h(k), ( h(k) + step ) % M, ( h(k) + 2*step ) % M, ...
그런데 선형 조사와 이차 조사에서 해시 함수가 같은 값이 나오면 동일한 형태로 빈 공간을 찾아다니므로
같은 값이 많이 발생하는 해시 함수일 경우 충돌이 잦음.
(예1) 크기(버켓)가 7인 해시 테이블에서,
첫 번째 해시 함수 = k mod 7
오버플로우 발생 시의 해시 함수는 step = 5 - (k mod 5)
- 입력 ( 8, 1, 9, 6, 13 ) 적용해보자
- 1단계 (8) : h(8) = 8 mod 7 = 1(저장)
- 2단계 (1) : h(1) = 1 mod 7 = 1(충돌발생)
- ( h(1) + step ) mod 7 = ( 1 + (5 - (1 mod 5)) ) mod 7 = (1 + 4) % 7 = 5(저장)
- 1에 대해 step 이 4이다.
- 3단계 (9) : h(9) = 9 mod 7 = 2(저장)
- 4단계 (6) : h(6) = 6 mod 7 = 6(저장)
- 5단계 (13) : h(13) = 13 mod 7 = 6(충돌 발생)
- (h(13)+step) mod 7 = (6 + 5-(13mod5)) mod 7 = 1(충돌발생)
- 13에 대해 step이 2이다.
- (h(13)+2*step)) mod 7 = (6 + 2*2) mod 7 = 3(저장)
아래의 테이블로 저장이 된다.
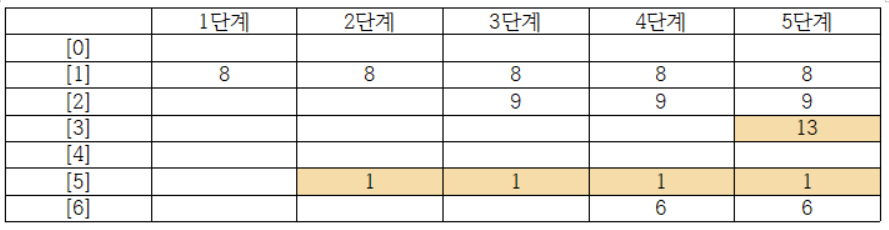
체이닝(chaining)로 저장하기
- 오버 플로우 문제를 연결 리스트로 해결하는 방법이다.
- 각 버켓에 고정된 슬롯이 할당되어 있지 않아 유용하다.
- 각 버켓에 삽입과 삭제가 용이한 연결 리스트 할당
- 버켓 내에서는 연결 리스트 순차 탐색
(예) 크기가 7인 해시 테이블에서
해시 함수 h(k) = k mod 7의 해시 함수
입력 ( 8, 1, 9 , 7, 13) 적용
- 1단계 (8) : h(8) = 8 mod 7 = 1(저장)
- 2단계 (1) : h(1) = 1 mod 7 = 1(충돌 발생 -> 새로운 노드 생성해 저장)
- 3단계 (9) : h(9) = 9 mod 7 = 2(저장)
- 4단계 (6) : h(6) = 6 mod 7 = 6(저장)
- 5단계 (13) : h(13) = 13 mod 7 = 6(충돌 발생 -> 새로운 노드 생성해 저장)
아래와 같은 그림으로 완성된다.

'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] AVL 트리와 탐색 (0) | 2022.06.04 |
|---|---|
| [자료구조] 우선순위 큐와 힙 (0) | 2022.05.25 |
| [자료구조] 이진 탐색 트리의 삽입,삭제 (재귀함수) (0) | 2022.05.16 |
| [자료구조] 이진 탐색 트리 삭제연산 (반복문) (0) | 2022.05.11 |
| [자료구조] 이진 탐색 트리 (탐색, 삽입) (0) | 2022.05.09 |




