쌓고 쌓다
[자료구조] 이진 탐색 트리 (탐색, 삽입) 본문
이진트리의 노드 개수 구하기
- 탐색 트리 안의 노드의 개수를 계산해준다.
- 각각의 서브 트리에 대하여 순환 호출, 반환 되는 값에 1을 더해 반환
int get_node_count(TreeNode* node)
{
int count = 0;
if (node != NULL)
{
count = 1
+ get_node_count(node->left)
+ get_node_count(node->right);
}
return count;
}
처음에 루트를 전달하면 총 6이 반한되어 나온다.
이진트리의 높이 구하기
- 서브 트리에 대하여 순환 호출하고 반환 값 중에서 최댓값을 반환해준다.
int get_height(TreeNode* node)
{
int height = 0;
if (node != NULL)
{
height = 1 + max(get_height(node->left), get_height(node->right));
}
return height;
}
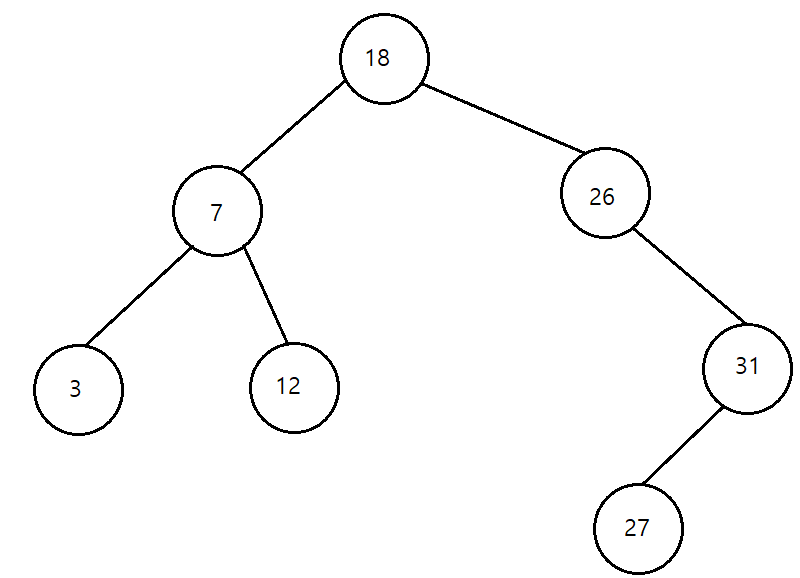
이진 탐색 트리
- 탐색작업을 효율적으로 하기 위한 자료구조
- key(왼쪽 서브 트리)<=key(루트 노드)<=key(오른쪽 서브 트리)
- 이진 탐색을 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있음

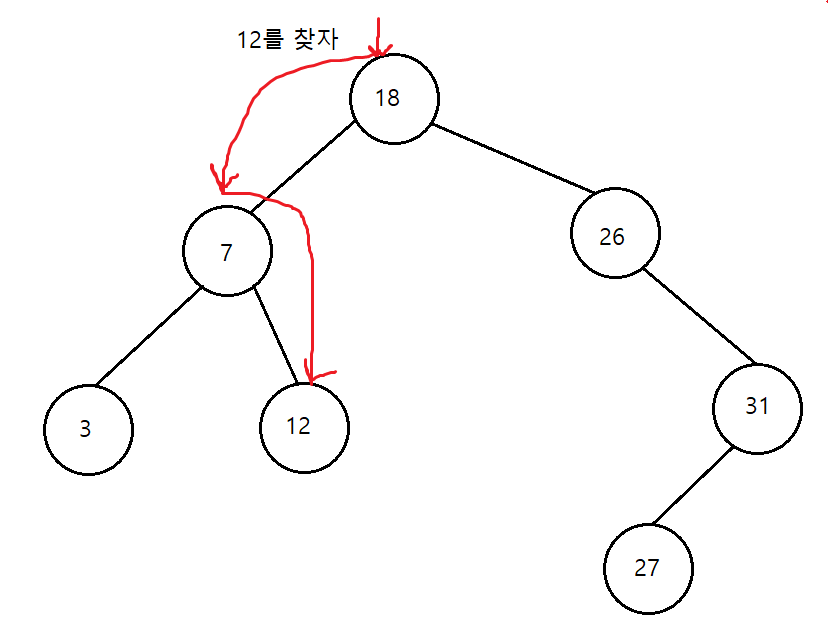
이진 탐색 트리 탐색 연산
- 비교한 결과가 같으면 탐색 성공
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 작으면 탐색은 이 노드의 왼쪽 자식을 기준으로 다시 시작.
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 크면 탐색은 이 노드의 오른쪽 자식을 기준으로 다시 시작.
이진 탐색 트리 - 순환적인 방법
TreeNode* search(TreeNode* node, int key)
{
if(node == NULL)
return NULL;
if (key == node->key)
return node;
else if (key < node->key)
return search(node->left, key);
else
return search(node->right, key);
}
이진탐색트리 - 반복 연산
TreeNode* search(TreeNode* node, int key)
{
while (node != NULL)
{
if (key == node->key)
return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL;
}
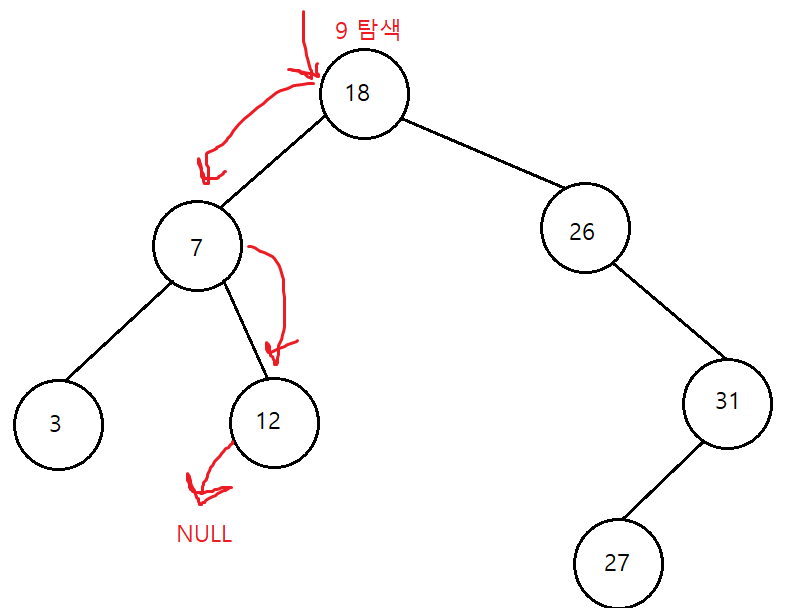
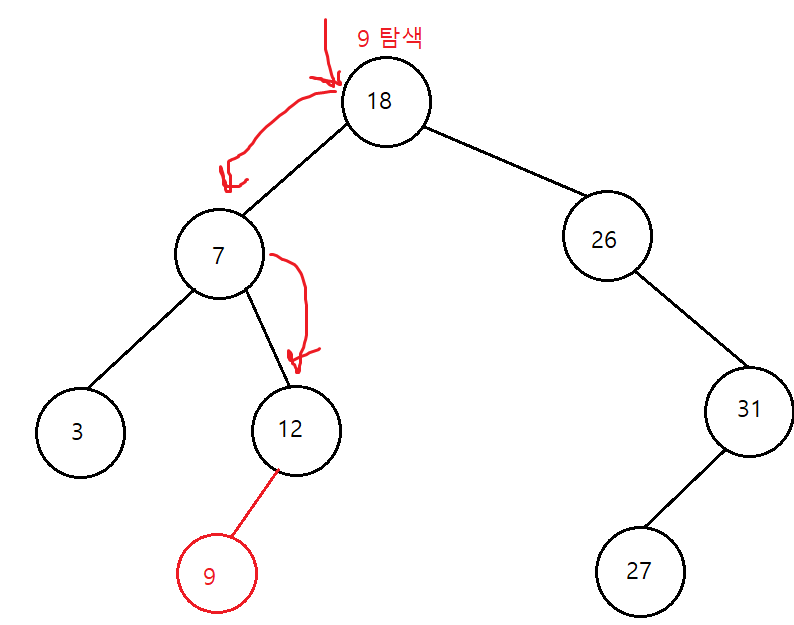
이진 탐색 트리 삽입 연산
- 원소 삽입을 위해 먼저 탐색을 수행
- 탐색에 실패한 위치가 새로운 노드를 삽입하는 위치
void insert_node(TreeNode** root, int key)
{
TreeNode* p, * c; // 부모, 현재 노드
TreeNode* n; // 새로운 노드
c = *root;
p = NULL;
while (c != NULL)
{
// 중복인경우 삽입X
if (key == c->key)
return;
p = c;
if (key < c->key)
c = c->left;
else
c = c->right;
}
n = (TreeNode*)malloc(sizeof(TreeNode));
if (n == NULL)
return;
n->key = key;
n->left = n->right = NULL;
// p가 NULL인 경우 트리가 비어 있는것임
// 트리에 1개라도 있다면 p는 그것을 가리키게 됨
if (p != NULL) {
if (key < p->key)
p->left = n;
else
p->right = n;
}
else
*root = n;
}'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] 이진 탐색 트리의 삽입,삭제 (재귀함수) (0) | 2022.05.16 |
|---|---|
| [자료구조] 이진 탐색 트리 삭제연산 (반복문) (0) | 2022.05.11 |
| [자료구조] 이진 트리의 순회 (0) | 2022.05.04 |
| [자료구조] 이진 트리 (0) | 2022.05.04 |
| [자료구조] 트리 용어 (0) | 2022.05.03 |





