쌓고 쌓다
[자료구조] 이진 트리의 순회 본문
순회 방법
- 전위 순회(preorder traversal) : 루트노드->Left->Right 방문, VLR
- 중위 순회(inorder traversal) : Left->루트노드->Right, LVR
- 후위 순회(postorder traversal) : Left->Right->루트노드, LRV
- _L_R_ : L R은 고정적이고 V의 위치에 따라 순회 방식이 정해진다. _를 선택하여 V 삽입

전위 순회 (preorder traversal)
: 루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리

// 전위 순회
void preorder(TreeNode* root) {
if (root)
{
printf("%d", root->data); // 루트 노드 방문
preorder(root->left); // 왼쪽 서브 트리 방문
preorder(root->right); // 오른쪽 서브 트리 방문
}
}
중위 순회(inorder traversal)
: 왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리

// 중위 순회
void inorder(TreeNode* root)
{
if (root)
{
inorder(root->left); //왼쪽 서브 트리 방문
printf("%d", root->data); //루트 노드 방문
inorder(root->right); // 오른쪽 서브 트리 방문
}
}
중위 순회 응용으로 수식 트리가 있다.

후위 순회(postorder traversal)
: 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드
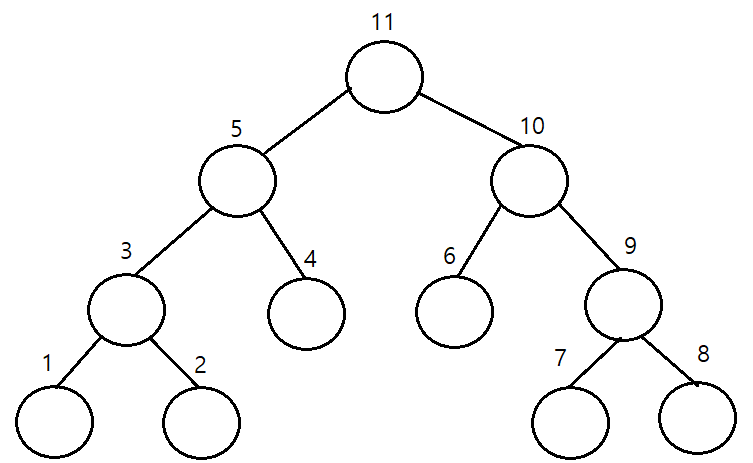
//후위 순회
void postorder(TreeNode* root)
{
if (root)
{
postorder(root->left); // 왼쪽 서브 트리 방문
postorder(root->right); // 오른쪽 서브 트리 방문
printf("%d", root->data); // 루트 노드 방문
}
}
레벨 순회
: 레벨 순으로 각 노드를 순회한다. 지금까지의 순회는 스택을 사용했고 레벨 순회는 큐를 사용한다.
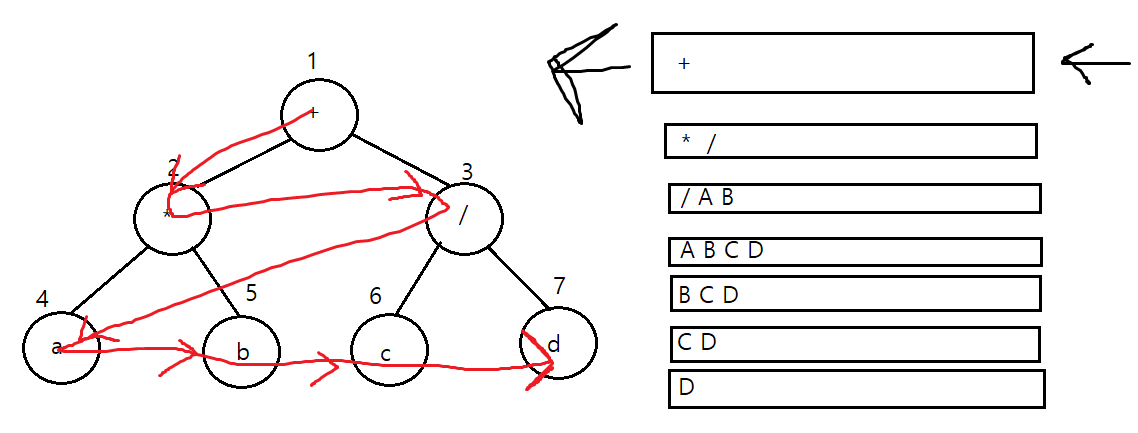
enqueue(&q, item)
q -> rear = q->rear+1 % MAX_SIZE
q->queue[q->rear]=item;
dequeue(&q)
q->front = q->front+1 % MAX_SIZE
return q->queue[q->front]
'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] 이진 탐색 트리 삭제연산 (반복문) (0) | 2022.05.11 |
|---|---|
| [자료구조] 이진 탐색 트리 (탐색, 삽입) (0) | 2022.05.09 |
| [자료구조] 이진 트리 (0) | 2022.05.04 |
| [자료구조] 트리 용어 (0) | 2022.05.03 |
| [자료구조] 리스트 (0) | 2022.04.06 |
Comments





