쌓고 쌓다
최소 공통 조상 알고리즘(LCA, Lowest Common Ancestor) 본문
(1) 정점 A, B의 LCA는 A, B를 자식으로 하는 가장 깊은 노드
(2) A가 B의 자식이라면 A와 B의 LCA는 B가 될 수 있다.
각각 해당하는 트리의 그림을 보자.

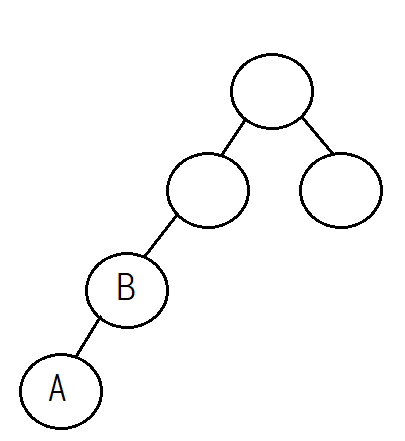
(1)의 경우
위로 푸른색의 노드들은 모두 A와 B의 공통된 부모이지만 진한 파란색의 노드가 가장 깊은 부모이자
LCA이다.
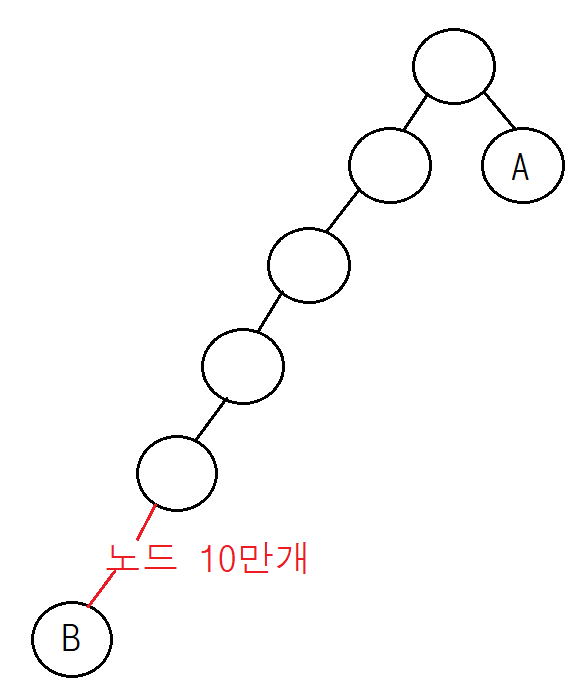
(2)의 경우
A와 B의 LCA는 B이다.
위의 그림을 보니 필요한 변수가 보인다.
- Tree를 저장할 인접 리스트
- 노드의 부모를 저장한 parent 배열
- 노드의 깊이를 저장할 depth 배열
단순히 한칸씩 올라가며 LCA를 찾는다면 아래와 같은 케이스에 엄청난 시간이 든다.
그래서 우리는 1, 2, 4, 8 ,16 ... 이런 방식으로 올라가자.
2의 승수로 올라가니 각 정점에 대해 1, 2, 4, 8... 번째 부모의 정보를 담을 배열이 필요하다.
여기서 2^0, 2^1, 2^2, 2^3, ...번째 부모의 정보가 필요하다
-> parent[n][k] : n번째 노드의 k번째 부모
여기서 k번째 부모는 2의 k승이다.
k가 0이면 2^0인 1번째 부모
k가 1이면 2^1인 2번째 부모
k가 2이면 2^2인 4번째 부모
k가 3이면 2^3인 8번째 부모이다.
여기서 배열 parent[n][k]를 만들 때 k의 최대 크기는
n=2^k 이므로 log2n=k 즉 k=log2에n이다.
안 나누어 떨어질 수 있으니 k가 2.XX일때 올림을 해주자 K는 3이다.
이제 parent 배열과 depth 배열을 완성시켜 보자.
먼저 루트를 시작으로 아래의 함수를 시작해주자
vector<int> v[100001];
-> v[i][j] : 노드 i의 j번째 연결된 노드의 정보
void DFS(int cur)
{
for (int i = 0; i < v[cur].size(); i++)
{
int next = v[cur][i];
if (depth[next] == -1)
{
parent[next][0] = cur;
depth[next] = depth[cur] + 1;
DFS(next);
}
}
}
DFS(1);루트가 1이라면 1을 시작으로
연결된 노드들을 방문하며 부모와 깊이를 갱신해줄 것이다.
next에 현재 노드와 연결된 노드의 정보를 담고
next의 2^0번째 부모는 cur이므로
parent[next]에 2^0번째 부모는 cur이다. -> parent[next][0] = cur
next의 깊이는 cur 깊이의 +1이다.
DFS를 통해 트리 아래로 내려간다.
이제 1번째 부모 정보 parent[][0]를 갱신해줬으니 2, 4, 8, ..번째 부모 정보도 갱신해주자
void connect()
{
for (int k = 1; k < 17; k++)
{
for (int cur = 1; cur <= N; cur++)
parent[cur][k] = parent[parent[cur][k - 1]][k-1];
}
}2^k번째 부모를 갱신해주어 나갈 건데
1부터 16까지 할 것이다
( 왜냐하면 10만 개의 노드를 기준으로 log2에10만은 16.61이므로 k는 17로 parent[100001][17]로 할당되었기 때문이다.)
노드가 10만 개 이므로 2^16은 65536이고 2^17은 131072이므로 최하위에서 취상위까지 부모 정보를 담을 수 있다.)
차근차근 k=1부터 현재 모든 노드의 부모를 차근차근 올라가 갱신해준다.
parent[cur][k] = parent[parent[cur][k - 1]][k-1];현재 cur의 2번째 부모는 cur의 1번째 부모의 1번째 부모이다.
아래의 그림을 보고 이해하자.

그럼 현재 cur의 4번째 부모는 cur의 2번째 부모의 2번째 부모이겠지요.
따라서 cur의 2^k번째 부모는 cur의 2^k-1번째 부모의 2^k-1번째 부모이다.
그래서 위의 식이 나온 겁니다.
cur의 2^k-1번째 부모 -> parent[cur][k - 1]
의 2^k-1번째 부모 -> parent[parent[cur][k - 1]][k-1]
이제 LCA를 어떻게 찾아야 할까?
1. 두 정점의 깊이를 같게 하자.
2. 부모가 같은 정점에 도달할 때까지 이동하자.
먼저 1번을 하기 위해 아래와 같은 함수를 작성합니다.
nt LCA(int a, int b) {
// 깊이가 더 큰게 a로 오게
if (depth[a] < depth[b])
{
int temp = a;
a = b;
b = temp;
}
int diff = depth[a] - depth[b];
for (int i = 0; diff != 0; i++)
{
if (diff % 2 == 1)
a = parent[a][i];
diff /= 2;
}
}a에 더 큰 깊이의 노드가 오게 만들고
두 깊이의 차를 구합니다.
이제 두 깊이 차이가 0이 될 때까지 뛸 겁니다.
점프를 2의 x승으로 점프를 뛰니 우리는 점프할 길이를 2진수로 나타낼 수 있습니다.
3칸을 점프하기 위해선 3을 2진수로 -> 11(2진수)입니다.
즉 2^0(1칸)칸 점프 1번, 2^1(2칸) 점프 1번 뛰면 됩니다.
11칸이면 2진수로 1011(2진수)이므로
2^0(1칸) 점프, 2^1(2칸), 2^3(8칸) 점프를 해주면 총 11칸을 점프할 수 있습니다.
그래서 diff가 0이 될 때까지 2^i칸을 점프 뛰고 diff /= 2를 하여 오른쪽 쉬프트(>>) 연산과 같은 효과를 냅니다.
이제 깊이가 같아졌으니 동시에 노드 a와 b를 움직입니다.
우리는 노드가 10만 개 이므로 k는 17이니 16부터 배열이 존재합니다.
즉, 16, 8, 4, 2, 1 이렇게 점프 뜁니다. 멀리멀리부터 먼저 뜁니다.
만약 점프를 뛰었더니 그곳에 부모가 -1이라면 트리(배열)에 벗어나는 공간이니 뛰면 안 됩니다.
공간 내에서 뛰어도 부모가 다르다면 뛰어 줍니다.
왜냐 뛰었더니 부모가 같다면 너무 점프를 많이 해서 이미 LCA를 지나쳐온 것이기 때문입니다.
그렇게 하여 마지막으로 1칸만 뛰어준다면 LCA를 구할 수 있습니다.
이것도 왜냐.. 우리가 구한 것은 부모가 달라지는 최초의 노드를 각각 구한 거기 때문에
여기서 한 깊이씩 올라가면 바로 부모가 같아지는 노드이기 때문입니다.
그것을 아래와 같이 코드를 덧붙여줍니다.
int LCA(int a, int b) {
// 깊이가 더 큰게 a로 오게
if (depth[a] < depth[b])
{
int temp = a;
a = b;
b = temp;
}
// 깊이를 맞추자 (1)
int diff = depth[a] - depth[b];
for (int i = 0; diff != 0; i++)
{
if (diff % 2 == 1)
a = parent[a][i];
diff /= 2;
}
// 깊이가 같아졌으니 뛰자 (2)
if (a != b)
{
for (int i = 16; i >= 0; i--)
{
if (parent[a][i] != -1 && parent[a][i] != parent[b][i])
{
a = parent[a][i];
b = parent[b][i];
}
}
a = parent[a][0];
// 위 라인을 지우고 return parent[b][0]; 해도 무방
}
return a;
}만약 높이를 맞췄더니 a와 b가 같다면 그냥 a를 return 해주면 됩니다.
젤 처음 소개한 트리의 예시중 (2)에 해당하기 때문입니다.
전체 코드
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
vector<int> v[100001];
int parent[100001][17]; // log2(100000) = 16.61 -> 17
int depth[100001];
int N,M;
void DFS(int cur)
{
for (int i = 0; i < v[cur].size(); i++)
{
int next = v[cur][i];
if (depth[next] == -1)
{
parent[next][0] = cur;
depth[next] = depth[cur] + 1;
DFS(next);
}
}
}
void connect()
{
for (int k = 1; k < 17; k++)
{
for (int cur = 1; cur <= N; cur++)
parent[cur][k] = parent[parent[cur][k - 1]][k-1];
}
}
int LCA(int a, int b) {
// 깊이가 더 큰게 a로 오게
if (depth[a] < depth[b])
{
int temp = a;
a = b;
b = temp;
}
int diff = depth[a] - depth[b];
for (int i = 0; diff != 0; i++)
{
if (diff % 2 == 1)
a = parent[a][i];
diff /= 2;
}
// 깊이가 같아졌으니 뛰자
if (a != b)
{
for (int i = 16; i >= 0; i--)
{
if (parent[a][i] != -1 && parent[a][i] != parent[b][i])
{
a = parent[a][i];
b = parent[b][i];
}
}
a = parent[a][0];
}
return a;
}
int main(void)
{
cin.tie(0);
ios_base::sync_with_stdio(0);
int a, b;
cin >> N;
fill(depth, depth + N + 1, -1);
depth[1] = 0;// root 노드
for (int i = 0; i < N-1; i++)
{
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
DFS(1);
connect();
cin >> M;
for (int i = 0; i < M; i++)
{
cin >> a >> b;
cout << LCA(a, b) << "\n";
}
}
이 알고리즘으로 아래의 문제를 제한시간내에 풀 수 있다.
'알고리즘 > 개념' 카테고리의 다른 글
| 에라토스테네스의 체 C++ 구현 코드 (0) | 2022.07.12 |
|---|---|
| 허프만 코드 (0) | 2022.06.04 |
| 후위 표기식 계산 - 스택 활용 (0) | 2022.03.28 |
| 후위 표기식 변환 - 스택 활용 (0) | 2022.03.28 |
| 올바른 괄호 판별 - 스택 활용 (2) | 2022.03.28 |

