쌓고 쌓다
[백준] 센서 2212번 C++ 풀이 본문
https://www.acmicpc.net/problem/2212
2212번: 센서
첫째 줄에 센서의 개수 N(1 ≤ N ≤ 10,000), 둘째 줄에 집중국의 개수 K(1 ≤ K ≤ 1000)가 주어진다. 셋째 줄에는 N개의 센서의 좌표가 한 개의 정수로 N개 주어진다. 각 좌표 사이에는 빈 칸이 하나 있
www.acmicpc.net
전체 코드(1)
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N, K;
vector<int> v;
vector<int> v2;
int main(void)
{
cin >> N;
cin >> K;
if (K >= N)
{
cout <<"0";
return 0;
}
for (int i = 0; i < N; i++)
{
int n;
cin >> n;
v.push_back(n);
}
sort(v.begin(), v.end());
for (int i = 0; i < N - 1; i++)
v2.push_back(v[i + 1] - v[i]);
sort(v2.begin(), v2.end());
int res = 0;
for (int i = 0; i < v2.size() - (K - 1); i++)
res += v2[i];
cout << res;
}
코드(2)
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int N, K;
vector<int> v;
vector<int> v2;
int main(void)
{
cin >> N;
cin >> K;
for (int i = 0; i < N; i++)
{
int n;
cin >> n;
v.push_back(n);
}
sort(v.begin(), v.end());
for (int i = 0; i < N - 1; i++)
v2.push_back(v[i + 1] - v[i]);
sort(v2.begin(), v2.end());
int res = 0;
for (int i = 0; i < v2.size() - (K - 1)&&!v2.empty(); i++)
res += v2[i];
cout << res;
}
N>=K인 경우에 대해 예외를 처리해주어야 한다.
코드(1)에서는 처음부터 N>=K인 경우 최소거리는 0이 되니 0을 출력해주고
코드(2)에서는 N=1, K=2인 경우 v2가 비었지만 v2[0]을 접근하기에 에러가 난다, 즉 !v2.empty()를 추가
그 외에는 두 코드 모두 동일하다.
풀이방법으로는 크게 본다면 두 센서 간의 차이가 큰 것을 빼주면 합이 최소가 된다.
즉, 집중국을 모두 사용하는것이 최소합을 만드는 방법이고
K개의 집중국을 설치할 수 있으니 센서를 가까운 애들끼리 K개의 집합으로 나누어 준다면
영역의 길이 합이 최소가 된다.
따라서 두 센서의 거리가 큰 애들을 기준으로 끊어준다면(영역을 나누어 준다면) 길이의 합이 최소가 된다.
일단 센서 N개의 좌표를 입력 받는다.
그리고 그것을 정렬한다.
센서의 좌표 사이의 거리를 모두 구한다.
그것을 또 정렬한다.
그것 중 사이의 좌표 거리가 큰 것 K-1개를 빼주면 최소가 된다.
예로 2개의 집중국이 있다면 거리차가 큰 1개를 끊어준다면 길이가 최소가 될 것
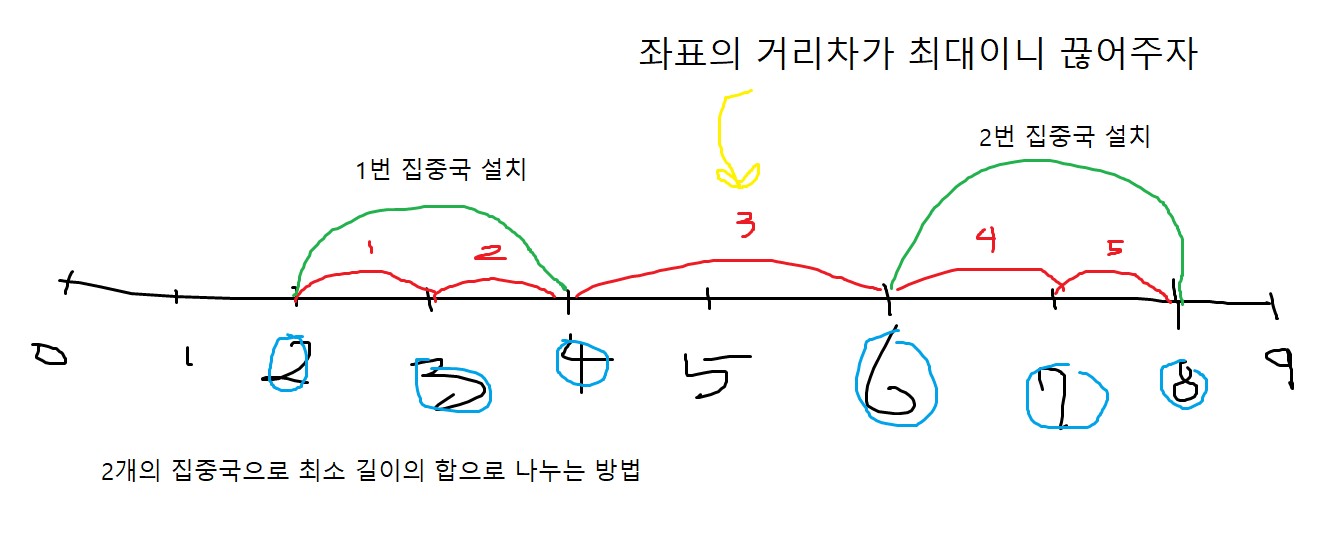
K개의 집중국이 있다면 큰 거리차 K-1개를 빼준다면 K개의 영역으로 최소합으로 나누어진다.
sort(v.begin(), v.end());
for (int i = 0; i < N - 1; i++)
v2.push_back(v[i + 1] - v[i]);모든 센서의 거리차를 구하는 과정( 정렬을 먼저 하여 가까운 센서끼리 거리차를 구한다)
sort(v2.begin(), v2.end());
int res = 0;
for (int i = 0; i < v2.size() - (K - 1); i++)
res += v2[i];v2에는 거리차 들이 들어있는데
v2는 오름차순으로 정렬되어있으므로 끝에 젤 큰 거리차 K-1개를 빼준다면 최소합을 구할 수 있다.
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 카드 놓기 5568번 C++ 풀이 (0) | 2022.05.02 |
|---|---|
| [백준] A와 B 12904번 C++ 풀이 (0) | 2022.05.01 |
| [백준] 친구비 16562번 C++ 풀이 (0) | 2022.04.29 |
| [백준] 과제 13904번 C++ 풀이 (0) | 2022.04.28 |
| [백준] 트럭 13335번 C++ 풀이 (0) | 2022.04.09 |
