[백준] 행성 터널 2887번 C++ 풀이
https://www.acmicpc.net/problem/2887
2887번: 행성 터널
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이
www.acmicpc.net
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
int parent[100001];
int N,res;
vector<pair<int,int>> v[3]; // 좌표,i번째 행성
vector<pair<int, pair<int, int>>> planet; // dis,A번째 행성,B번째 행성
int Find(int x)
{
if (parent[x] == x)
return x;
return parent[x] = Find(parent[x]);
}
bool SameParent(int a, int b)
{
a = Find(a);
b = Find(b);
if (a != b)
return false;
else
return true;
}
void Union(int a, int b)
{
a = Find(a);
b = Find(b);
if (a != b)
parent[a] = b;
}
int main(void)
{
int x, y, z;
cin >> N;
for (int i = 0; i < N; i++)
{
cin >> x >> y >> z;
v[0].push_back(make_pair(x, i));
v[1].push_back(make_pair(y, i));
v[2].push_back(make_pair(z, i));
parent[i] = i;
}
sort(v[0].begin(), v[0].end());
sort(v[1].begin(), v[1].end());
sort(v[2].begin(), v[2].end());
for (int i = 0; i < N - 1; i++)
{
planet.push_back(make_pair(abs(v[0][i].first - v[0][i + 1].first), make_pair(v[0][i].second, v[0][i+1].second)));
planet.push_back(make_pair(abs(v[1][i].first - v[1][i + 1].first), make_pair(v[1][i].second, v[1][i + 1].second)));
planet.push_back(make_pair(abs(v[2][i].first - v[2][i + 1].first), make_pair(v[2][i].second, v[2][i + 1].second)));
}
sort(planet.begin(), planet.end());
for (int i = 0; i < planet.size(); i++)
{
if (!SameParent(planet[i].second.first, planet[i].second.second))
{
res += planet[i].first;
Union(planet[i].second.first, planet[i].second.second);
}
}
cout << res;
}
코드의 부분부분 파트별로 나눠 해설해드리겠습니다~
해설을 보기 전에 핵심으로 최소 스패닝 트리로 푸는데 모든 간선의 정보가 필요가 없다는 것을 인지하고
간선의 후보들만 뽑아내서 풀면 풀어집니다.
그 후보들을 어떻게 뽑아낼지 고민하시면 됩니다.
부분부분 코드 상세 풀이
vector<pair<int,int>> v[3];
vector<pair<int, pair<int, int>>> planet;v가 무엇을 담는 벡터인가? - > v[0]에는 x좌표, v[1]에는 y좌표, v[2]에는 z좌표를 담을 것입니다
pair<int,int>는 해당 좌표와 몇 번째 행성인지를 담습니다.
0번째 행성의 x좌표는 v[0]에 (x좌표,0)이 담길 것이고
1번째 행성의 x좌표는 v[0]에 (x좌표,1)이 담길것입니다.
planet은 무엇인가? -> 인자 순서대로 (A번째 행성과 B번째의 행성거리, A행성번호, B행성번호)가 담깁니다
1번째 행성과 3번째 행성이라면 (1번째 행성 x좌표 - 3번째 행성 x좌표, 1, 3) 이 담깁니다.
int Find(int x)
{
if (parent[x] == x)
return x;
return parent[x] = Find(parent[x]);
}
bool SameParent(int a, int b)
{
a = Find(a);
b = Find(b);
if (a != b)
return false;
else
return true;
}
void Union(int a, int b)
{
a = Find(a);
b = Find(b);
if (a != b)
parent[a] = b;
}Find, SameParent, Union 함수는 최소 스패닝 트리를 위한 함수들이라 따로 알고리즘을 학습하시면 이해가 가십니다~
for (int i = 0; i < N; i++)
{
cin >> x >> y >> z;
v[0].push_back(make_pair(x, i));
v[1].push_back(make_pair(y, i));
v[2].push_back(make_pair(z, i));
parent[i] = i;
}i번째 행성의 x y z 를 v에 담아주시고 최소 스패닝 트리의 크루스칼 알고리즘을 위한 parent 부모를 자신으로 초기화합니다.
sort(v[0].begin(), v[0].end());
sort(v[1].begin(), v[1].end());
sort(v[2].begin(), v[2].end());각 x y z 좌표에 대해 인접한 좌표에 대해서만 최소 스패닝 트리의 간선으로 사용할 것입니다.
모든 간선은 메모리 초과가 나기 때문에 모든 간선은 담을 수 없고 인접한 행성, 즉 좌표가 가까운 애들끼리만 후보로 올려 보냅니다.
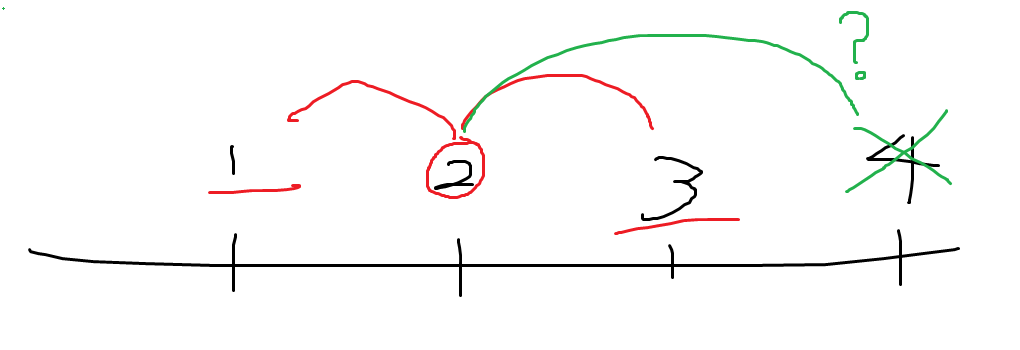
보시면 알겠지만 2번 행성의 경우 1과 3의 행성의 거리만 쓰면 될 텐데 왜냐? 인접하니깐 최소일 것입니다.
2와 4의 거리는 넘나 머니깐 후보로도 부적절하겠죠?? 볼 필요도 없다는 뜻.!
for (int i = 0; i < N - 1; i++)
{
planet.push_back(make_pair(abs(v[0][i].first - v[0][i + 1].first), make_pair(v[0][i].second, v[0][i+1].second)));
planet.push_back(make_pair(abs(v[1][i].first - v[1][i + 1].first), make_pair(v[1][i].second, v[1][i + 1].second)));
planet.push_back(make_pair(abs(v[2][i].first - v[2][i + 1].first), make_pair(v[2][i].second, v[2][i + 1].second)));
}위의 설명을 코드로 옮긴 것이 이것입니다
i번째의 경우 i+1번째 행성과의 거리만 planet에 넣어주면 됩니다.
i번째 행성과 저 멀리 5번째나 멀리 있는 i+5번째 행성과의 거리를 비교할 필요는 없겠죠??
planet에 거리와 각 행성이 몇 번째인지를 담아 줍니다.
sort(planet.begin(), planet.end());
for (int i = 0; i < planet.size(); i++)
{
if (!SameParent(planet[i].second.first, planet[i].second.second))
{
res += planet[i].first;
Union(planet[i].second.first, planet[i].second.second);
}
}크루스칼을 쓰기 위해 planet을 정렬해주고 같은 부모가 아니라면 연결해주고 비용을 추가해줍니다.