[백준] 트리의 순회 2263번 C++ 풀이

https://www.acmicpc.net/problem/2263

2263번: 트리의 순회

 

전체 코드

#include <iostream>
#include <vector>
using namespace std;
vector<int> inorder;
vector<int> postorder;
int Index[100001];
int N,root;
void preorder(int inStart, int inEnd, int postStart, int postEnd)
{
	if (inStart > inEnd || postStart > postEnd)
		return;

	int root = postorder[postEnd];
	int rootIndex = Index[root];
	int leftSize = rootIndex - inStart;
	int rightSize = inEnd - rootIndex;

	cout << root << " ";

	preorder(inStart, rootIndex-1, postStart, postStart + leftSize-1);
	preorder(rootIndex + 1, inEnd, postStart + leftSize, postEnd - 1);
}

int find(int x)
{
	for (int i = 0; i < N; i++)
	{
		if (inorder[i] == x)
		{
			return i;
		}
	}
}
int main(void)
{
	cin >> N;
	for (int i = 0; i < N; i++)
	{
		int num;
		cin >> num;
		inorder.push_back(num);
		Index[num] = i; // 중위 순회에서 num의 인덱스
	}
	for (int i = 0; i < N; i++)
	{
		int num;
		cin >> num;
		postorder.push_back(num);
	}
	preorder(0,N-1,0,N-1);

}

 

먼저 아래의 트리를 보자

 

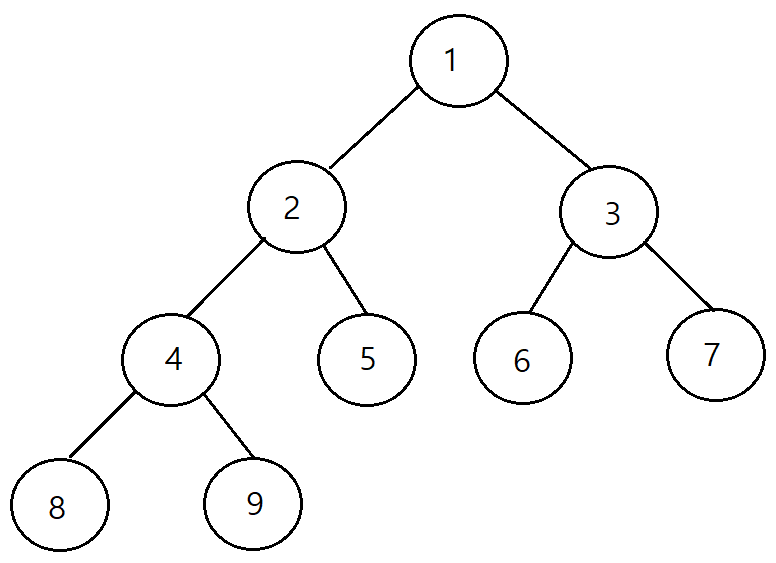
위의 트리에서 중위, 후위 순회는 아래와 같다.

여기서 후위순회의 마지막 노드는 항상 그 트리의 루트 노드이다.

중위 순회에서 루트 노드를 기준으로 왼쪽의 노드들은 왼쪽 서브 트리이고,

오른쪽의 노드들은 오른쪽 서브 트리의 노드들로 나눌 수 있다.

여기서 중위순회의 left 트리의 크기만큼 후위 순회에서 그 크기만큼은 left 트리이고

그 이후 바로 이어지는 노드들은 중위 순회 right 트리 사이즈만큼 right트리가 이어지고 루트 노드가 나온다.

여기서 이해를 위해 한번 더 트리를 나누어 보자.

아까 루트노드 1을 구해서 left와 right 트리를 나누었다.

그런데 또 나누어진 트리에서(후위 순회에서 나누어진 부분) 후위 순회를 보면 left 트리의 마지막 노드와

right의 마지막 노드가 또 루트의 노드가 된다.

 

 

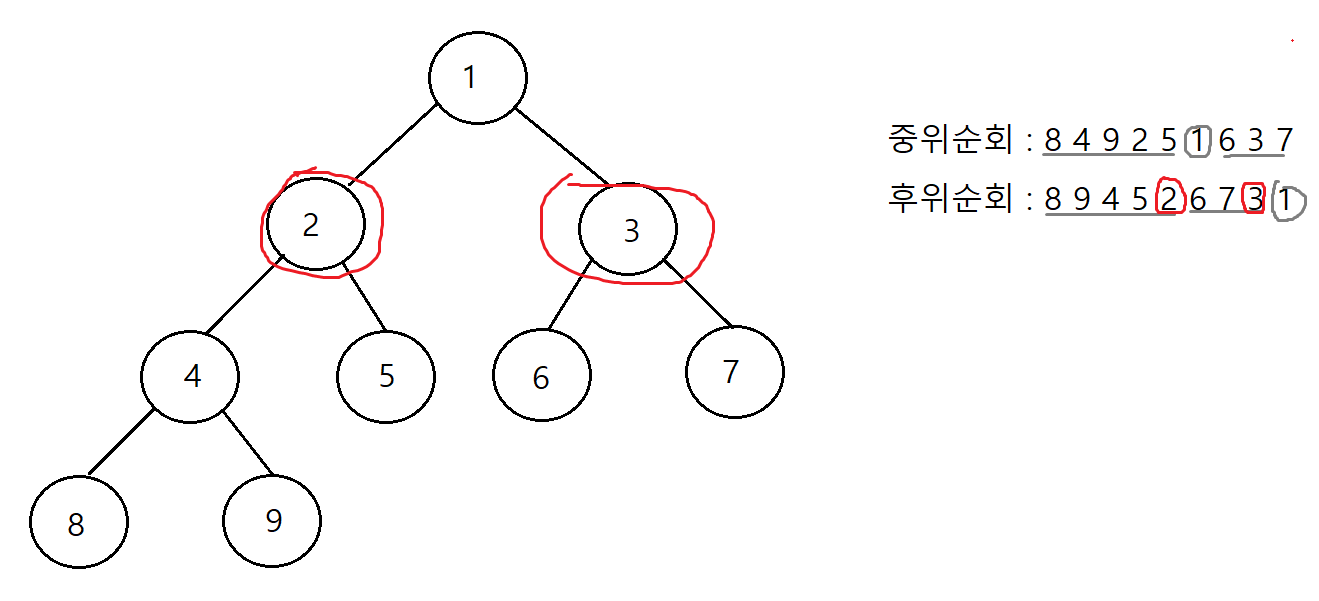
1의 기준으로 left, right의 루트 노드는 2와 3이 루트노드가 되니깐

2와 3을 기준으로 또 중위 순회에서

2를 기준으로 왼쪽은 left 서브트리, 오른쪽은 right 서브트리이다.

3을 기준으로 왼쪽으로는 left, 오른쪽은 right이다.

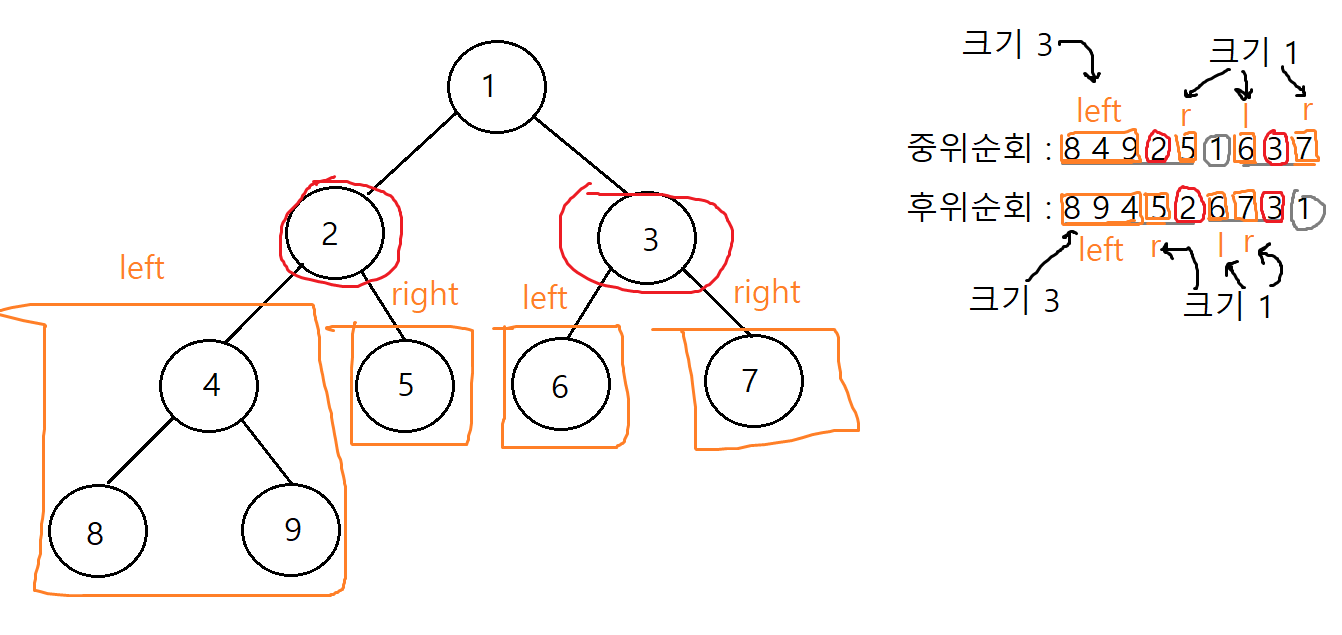
위의 그림에서 2를 기준으로 중위 순회에서 left 크기는 3, right의 크기는 1이다.

즉 후위순회에서 left로 3개의 노드가 나오고 바로이어서 right로 1개의 노드가 나오고 루트노드인 2가 나오는 순서 일 것이다.

 

3을 기준으로 left는 크기 1, right는 크기 1이니 이 3을 루트 노드로 하는 트리는 후위순회에서 left 크기인 1개만큼 노드 후 right 크기인 1 만큼 노드가 나오고 루트 노드인 3의 순서가 될 것이다.

 

이것 알고리즘을 통해 트리를 쪼개 쪼개서 전위순회를 구하면 된다.

 

코드 하나하나 설명을 시작하겠습니다.

for (int i = 0; i < N; i++)
{
	int num;
	cin >> num;
	inorder.push_back(num);
	Index[num] = i; // 중위 순회에서 num의 인덱스
}

먼저 inorder 벡터에 입력을 받은 자연수를 넣어줍니다.

그런데 우리는 위의 알고리즘을 사용하기 위해

자연수 num의 inorder에서의 인덱스 정보를 저장해둡시다.

 

for (int i = 0; i < N; i++)
{
	int num;
	cin >> num;
	postorder.push_back(num);
}
preorder(0,N-1,0,N-1);

postorder의 자연수 또한 넣어주고

preorder을 구하기 위한 함수를 실행합니다.

 

void preorder(int inStart, int inEnd, int postStart, int postEnd)

함수 원형을 보면 inorder의 시작 부분과 끝부분의 인덱스와

postorder의 시작과 끝 인덱스를 넣어줍니다.

첫 preorder에 들어갈 트리는 전체이므로 시작 인덱스 0과 끝 인덱스 N-1을 각각 넣어서 시작하겠죠.

 

int root = postorder[postEnd];
int rootIndex = Index[root];
int leftSize = rootIndex - inStart;
int rightSize = inEnd - rootIndex;

루트 노드의 값은 후위노드의 마지막 인덱스이고

루트 노드의 중위순회에서의 인덱스는 Index에 root 값을 넣어주면 나옵니다.

루트 노드를 기준으로 left 서브트리의 크기는 (루트 인덱스-시작인덱스)입니다.

right 서브트리의 크기는 (끝인덱스-root인덱스)입니다. <- 이 변수는 사용하지 않고 품

 

cout << root << " ";

preorder(inStart, rootIndex-1, postStart, postStart + leftSize-1); // 왼쪽 서브트리
preorder(rootIndex + 1, inEnd, postStart+leftSize, postEnd - 1); // 오른쪽 서브트리

각 함수를 실행할 때 root 노드를 출력해주고

왼쪽 오른쪽으로 쪼갠다.

 

아래와 같은 쪼개기 방법은 출력 초과를 일으킨다.

preorder(inStart, rootIndex-1, postStart, postStart + leftSize-1);
preorder(rootIndex + 1, inEnd, /*leftSize+1 <- 문제가 됨*/, postEnd - 1);

postStart라는 인덱스 값을 기준으로 오른쪽 서브트리 시작지점을 잡아줘야 한다

leftSize+1로하면 오른쪽 서브트리의 시작지점으로 될 것 같지만 정확한 인덱스가 안 들어가 출력 초과를 일으킴